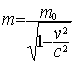Chapter 1
Tour Historique
J.P. Desclaux
15 Chemin du Billery,
F-38360 Sassenage, France
1. Introduction
We live in a world where the speed of light
is finite and does not depend upon the direction of observation as was proved
by the Michelson-Morley interferometer measurement in 1887. That experimental
evidence leads to many theoretical developments that culminate with A.
Einstein’s special theory of relativity at the beginning of the century. This
first "revolution" of the century in physics was rapidly followed by
a second one of equal importance for our understanding of the physical world at
the atomic scale. In 1913 Bohr had introduced a first description of the atom
that made it possible to predict the spectrum of hydrogen without introducing
free parameters, but one had to wait for another decade to see the birth of
quantum mechanics. After L. De Broglie suggested in 1924 that a wave should be
associated with any particle, W. Heisenberg and E. Schrödinger established the
theory of quantum mechanics in 1925-1926 which is still one the two pillars
(the second being the theory of relativity) of modern physics. The next
challenge was to unify these two theories at the atomic scale. This was
accomplished by P.A.M. Dirac in 1928 who could write in 1929: "This general theory of quantum
mechanics is now almost complete, the imperfections that still remain being in
connection with the exact fitting of the theory with relativity ideas. These
give rise to difficulties only when high-speed particles are involved, and are
therefore of no importance in the consideration of atomic and molecular
structure and ordinary chemical reactions, in which it is, indeed, usually
sufficiently accurate if one neglects relativity variation of mass with
velocity and assumes only Coulomb forces between the various electrons and
atomic nuclei. The underlying physical laws necessary for the mathematical
theory of a large part of physics and the whole of chemistry are thus
completely known, and the difficulty is only that the exact application of
these laws leads to equations much too complicated to be soluble. It therefore
becomes desirable that approximate practical methods of applying quantum
mechanics should be developed, which can lead to an explanation of the main
features of complex atomic systems without too much complications"
(P.A.M. Dirac, Proceedings of the Royal Society, 123A, 1929, P. 714)
As
it happens, people keep only a few words in mind and the above quotation has
sometimes been taken as a justification of ignoring relativistic effects in
atomic and molecular electronic structure. A more careful reading shows, on the
contrary, great perspicacity:
-
the need for "approximate
practical methods" for "equations much too complicated to be soluble" that could not be
fulfilled until computers become a reality about twenty years later,
-
or, from a more fundamental point of
view "the imperfections that still remain being in connection with the
exact fitting of the theory with relativity ideas". A still unsolved
problem since the general theory of relativity (gravitational force) and
quantum mechanics have not yet been unified. This is still considered as one
challenge for theoretical physics (see "What remains to be
discovered" by J. Maddox, Brockman, Inc. 1998).
The only missing important comment is the
need for the electromagnetic field to be also quantized (as suggested in the same year by W.
Heisenberg and W. Pauli) leading to the most accurate theory of physics:
Quantum Electrodynamics.
The
remaining sections of this chapter are devoted to a brief, and more or less historical
survey, of what has been done to fulfil the wish of Dirac of developing "approximate
practical methods" (the following chapters of this book will give much
more exhaustive descriptions of them) and show how far we have gone today from
what V.M. Burke and I.P. Grant could write in 1967: "Little attention
appears to have been paid to the effect of relativity on atomic wave functions
since White studied the matter in 1931".
2. Dirac equation
In this section we briefly review the main
properties of the Dirac equation that is the basic equation to start with to
build a relativistic effective Hamiltonian for atomic and molecular
calculations. This single particle equation, as already stated in the
introduction, was established in 1928 by P.A.M Dirac [1] as the Lorentz
invariant counterpart of the Schrödinger equation. On a note let us recall that
the first attempts to replace the Schrödinger equation by an equation
fulfilling the requirements of special relativity started just after quantum
mechanics was established. In 1926 the equation, now known as the Klein-Gordon
equation, was derived independently by several authors [2] but this equation
was historically discarded since it has solutions for probability densities r that can be either positive or negative. At that time no one
realized that any relativistic equation will describe both a particle and its
antiparticle and it was not until 1934 that the Klein-Gordon equation was
correctly reinterpreted by Pauli and Weisskopf [3] as the relativistic quantum
mechanical equation for spin zero particles. Ironically, the Dirac equation
exhibits, and we understand now why, the same pitfall but was rapidly accepted
since it explicitly includes the spin and also because of the prediction of the
existence of the positron experimentally discovered in 1932 by C. D. Anderson.
As required by special relativity, space
and time variables should appear in a symmetric way and this requirement is
most obvious in the covariant form of the Dirac equation:
|
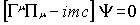
|
(1)
|
where m is the mass of the particle,
c the speed of light and the 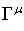 are matrices that
fulfil the commutation rule
are matrices that
fulfil the commutation rule
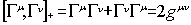 where
where 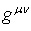 is the metric tensor
is the metric tensor
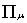 is the four-vector
is the four-vector
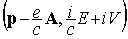
defined in terms of the momentum vector 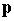 and energy E
of the particle and of the vector (
and energy E
of the particle and of the vector (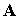 ) and scalar (
) and scalar (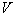 ) potentials of the external electromagnetic field. As for
all the remaining sections of this chapter we shall consider only time
independent scalar external fields, we rewrite Eq. (1) in the usual form:
) potentials of the external electromagnetic field. As for
all the remaining sections of this chapter we shall consider only time
independent scalar external fields, we rewrite Eq. (1) in the usual form:
|
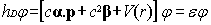
|
(2)
|
where from now on we use atomic units by
putting 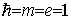 . In this system the speed of light c » 137 is the inverse of the fine structure constant. For the (4x4)
Dirac matrices a
and b we adopt the conventional
representation that is useful when considering the non-relativistic limit of
the Dirac equation. In this standard representation the components of a are expressed in terms of the
(2x2) Pauli matrices and b is taken to be diagonal, explicitly:
. In this system the speed of light c » 137 is the inverse of the fine structure constant. For the (4x4)
Dirac matrices a
and b we adopt the conventional
representation that is useful when considering the non-relativistic limit of
the Dirac equation. In this standard representation the components of a are expressed in terms of the
(2x2) Pauli matrices and b is taken to be diagonal, explicitly:
|
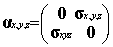
|
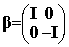
|
(3)
|
where I and 0 are respectively the (2x2) unit and zero matrices
and the Pauli matrices s have their usual definition:
The
eigenvalue spectrum of the Dirac equation in the Coulomb field of a nuclear
charge Z is sketched in Fig. 1. First one notices the presence of two
continua (one below -mc2 and the other above mc2)
instead of the single positive continuum of the Schrödinger equation. These two
continua are separated by a gap equal to 2mc2. A non-zero
value of the nuclear charge Z introduces bound states in this gap (Z>0
is illustrative of hydrogen, i.e. an electron bound to a proton, while Z<0
corresponds to positronium, i.e. a positron bound to an antiproton). The
negative continuum for electronic states was of concern at the early stage of
relativistic atomic structure theory and led Dirac to postulate that all states
of negative energy are occupied and form the physical vacuum. This was
an ad-hoc and empirically efficient way to insure atomic stability by
preventing radiative decay into the negative energy states. We shall see later
that there is no need to assume an infinite number of electrons in the vacuum.
Indeed, as already pointed out, a relativistic theory describes both a particle
and its antiparticle so that only the total charge of the system is conserved
but not the number of particles. For physical systems in which no
particle-antiparticle pairs are created we should add a constraint to take this
fact into account. We shall elaborate more on this point in the next section.
Fig 1 Schematic
Dirac spectrum for a Coulomb field
If we remember that the eigenvalues of the
Schrödinger equation are directly proportional to the mass m of a
particle while the expectation mean value <r> scales as 1/m,
we expect that the eigenvalues of the Dirac equation will show both an increase
in the binding energy of an electron and a contraction of the radial wave
functions towards the origin because of the relativistic increase in the mass
given by:
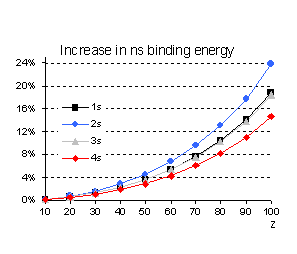
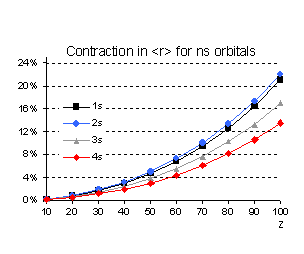
This is indeed the case as illustrated in
Fig. 2 for s orbitals. However, we should avoid oversimplified approximations,
like assuming that because the "classical velocity" of an electron is
a decreasing function of the principal quantum number n (<v2/c2>
= (Za)2/n),
relativistic corrections should be monotonically decreasing functions of n
as well. From the analytical solution of the Dirac equation for a point nucleus
of charge Z it is straightforward to show that the binding energy of the
s electrons is given to lowest order in (Z/c) by:
from which it is obvious that the
relativistic increase in the binding energy (the second term in the bracket) is
not a monotonic function of n since it is greater for n=2 than
for n=1 while it gives the same correction both for n=1 and n=3.
Fig 2 Relativistic corrections for
hydrogenic s orbitals (as percentage of the non relativistic value).
Even if the n scaling is different
for the expectation value of r we also notice that, percentage wise, the 2s
orbital contracts more than the 1s. These relative changes between the results
given by the Schrödinger and Dirac equations hold when solving both equations for
the same potential. But, for a many electron system, the self-consistent field
effects change this simple picture quite significantly as we shall illustrate
later.
To
conclude this short introduction to the Dirac equation, let us summarize the
main results for one-electron systems:
-
relativistic binding energies are
larger than non relativistic ones, the largest increase is for an electron with
total angular momentum j=1/2,
-
the non relativistic orbital
degeneracy of the energy is partially removed because of the explicit inclusion
of the spin-orbit coupling,
-
radial electron density contracts
towards the nucleus,
-
because the Dirac wave functions have
two components (see next chapter) with radial nodes interlaced, the radial
electron density vanishes only at the origin and infinity but never at a finite
distance.
If, as stated above, orbital degeneracy is
partially removed, it remains that for a given value of the principal quantum
number n, levels with the same j value but with different orbital
angular momenta (like 2s and 2p1/2) are degenerate. This is due to
the fact that the original Dirac theory treats the electromagnetic field as a
classical field. Quantization of the electromagnetic field lifts this
degeneracy as was observed for the first time by Lamb and Retherford [4] who
measured a splitting (Lamb shift) of 0.033 cm-1 in hydrogen.
The lowest order corrections introduced by the quantization of the
electromagnetic field are given by the two Feynman diagrams of Fig. 3 in which
the double lines stand for a bound electron in the Coulomb field of the
nucleus.
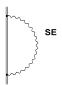

Fig 3 Lowest order
QED corrections
The
first diagram (labelled SE) corresponds to the emission and reabsorption of a
virtual photon by an electron and describes the interaction of an electron with
its own radiation field. This contribution, known as the self-energy
correction, is the dominant quantum electrodynamical (QED) contribution to the
Lamb shift for electrons. The vacuum polarization given by the second diagram
(VP) is associated with the interaction of the electron with a virtual
electron-positron pair (remember that the Dirac equation conserves the charge
of the system but not the number of particles). QED effects in atoms will be
discussed in more detail in chapter 8. It is nevertheless worthwhile to give
the order of magnitude for QED effects for a high Z hydrogenic 1s electron.
Table 1
Contributions to
1s electron binding energy in U+91
|
Contribution
|
Value (in eV)
|
|
Point nucleus
Dirac equation
|
-132 279.61
|
|
Finite nucleus
correction
|
198.82
|
|
Self Energy
|
355.05
|
|
Vacuum
Polarization
|
-88.60
|
|
Higher order QED
corrections
|
-0.64
|
|
Nuclear recoil
and nuclear polarization
|
0.28
|
|
Reduced mass
correction
|
-0.30
|
|
Lamb shift (i.e.
sum of all above corrections)
|
464.61
|
|
1s binding
energy
|
-131 815.00
|
From the values given in the above table it
is obvious that the finite nucleus and QED corrections contribute with the same
order of magnitude to the Lamb shift in a heavy atom. The uncertainty in the
theoretical value comes not only from yet uncalculated very high order QED
contributions (estimated to be less few tenths of an eV) but also from less
well known nuclear parameters of uranium that can amount to an uncertainty of
about 0.3 eV. Up till now the best experimental value for the 1s Lamb shift in
U91+ obtained at the GSI [5] is 468±13 eV. This value is still an order of magnitude too imprecise to
allow QED to be tested in high Coulomb fields where Za is not a small parameter.
3. many electron systems
3.1 Defining an effective Hamiltonian
Let us now consider the extension of the
relativistic Dirac theory to many electron systems. As pointed out in the
previous section, only the total charge is conserved but not the number of
particles, we can thus formally write the Hamiltonian as:
|
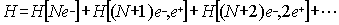
|
(4)
|
and for atoms and molecules restrict
ourselves to a physical system with N electrons without any positron. This is
known as the no-pair approach [6,7] and formally implies that the Hamiltonian
must include some kind of constraint to prevent the creation of pairs of
electron-positron and to avoid the so-called Brown Ravenhall [8] "disease"
arising from the fact that discrete levels would be embedded in a sea of
continuous levels. If this would be the case the discrete levels will
autoionize in conflict with the physical reality that atoms and molecules are
stable. To illustrate where the problem come from (the reader should not be
surprised that the negative energy states found in the one electron case will
not disappear for many electron systems) let us consider a two-electron atom.
The "natural" extension of the Dirac theory would be to consider the
Hamiltonian:
|
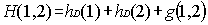
|
(5)
|
where the one electron Hamiltonians hD
are given by Eq. (2) and g(1,2) is any kind of electron-electron
interaction. To eliminate electron-positron pairs the use of a projection
operator has been advocated to ensure that the two-body interaction g(1,2)
connects only positive energy states among themselves. This amounts to replace
Eq. (5) by
|
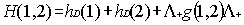
|
(6)
|
where the positive energy state projection
operator 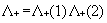 is defined in terms
of one electron positive energy eigenfunctions (for both discrete and continuum
eigenvalues) of some one-electron Hamiltonian by:
is defined in terms
of one electron positive energy eigenfunctions (for both discrete and continuum
eigenvalues) of some one-electron Hamiltonian by:
|
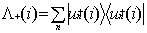
|
(7)
|
The choice of the one-electron Hamiltonian
that defines the  is far from being
trivial. Indeed negative and positive energy states have no absolute definition
and can be assigned only after a given potential has been chosen (no potential
for free electron, nuclear potential for hydrogenic solutions or any other). As
for any potential all the eigenstates (both positive and negative) of the Dirac
equation form a complete basis, the subspace of positive energy eigenstates in
a given potential will include part of the negative subspace associated to
another potential. Consequently, inconsistent use of un basis
sets can lead to meaningless results. Thus, when performing Hartree-Fock
calculations the un functions must be the Fock eigenstates
and the projection operator of Eq. (7) reduces to the identity operator. This
is in agreement with the result obtained by Mittleman [7] who investigated,
from a variational point of view, the best possible choice for the un
when the total wave function is restricted to a single determinant. The
conclusion is that the use of Eq. (5) without a projection operator is
justified provided that we keep only its positive energy solutions. Studying
the self-adjointness of the Dirac operator and the properties of the
quadratically integrable one-electron Dirac wave functions I.P. Grant [9]
reached the same conclusion.
is far from being
trivial. Indeed negative and positive energy states have no absolute definition
and can be assigned only after a given potential has been chosen (no potential
for free electron, nuclear potential for hydrogenic solutions or any other). As
for any potential all the eigenstates (both positive and negative) of the Dirac
equation form a complete basis, the subspace of positive energy eigenstates in
a given potential will include part of the negative subspace associated to
another potential. Consequently, inconsistent use of un basis
sets can lead to meaningless results. Thus, when performing Hartree-Fock
calculations the un functions must be the Fock eigenstates
and the projection operator of Eq. (7) reduces to the identity operator. This
is in agreement with the result obtained by Mittleman [7] who investigated,
from a variational point of view, the best possible choice for the un
when the total wave function is restricted to a single determinant. The
conclusion is that the use of Eq. (5) without a projection operator is
justified provided that we keep only its positive energy solutions. Studying
the self-adjointness of the Dirac operator and the properties of the
quadratically integrable one-electron Dirac wave functions I.P. Grant [9]
reached the same conclusion.
At
the beginning stage of relativistic electronic structure theory the negative
energy continuum was sometimes regarded to be responsible for the failure to
produce upper bounds in the total energy leading to the so-called
"variational collapse" in molecular calculations when basis sets were
applied. This attractive explanation was unfortunately too limited to explain
also the appearance of spurious solutions. Indeed, both the existence of
spurious solutions and the lack of convergence to expected levels can be traced
back to originate from poor basis sets and bad finite matrix representations of
the operators (in particular for the kinetic energy). For an extensive
discussion see Ref. 10.
3.2 Electron-electron interaction
Dealing with electrons we know that the
dominant interaction between them is the Coulomb repulsion corrected, because
electrons are fermions, by interactions induced by their spin. The spin-orbit
interaction is already included in the one-electron Dirac Hamiltonian but the
two-electron interaction should also include interactions classically known as
spin-other-orbit, spin-spin etc… Furthermore a relativistic theory should
incorporate the fact that the speed of light being finite there is no
instantaneous interaction between particles. The most common way of deriving an
effective Hamiltonian for a many electron system is to start from the Furry
[11] bound interaction picture. A more detailed discussion is given in chapter
8 and we just concentrate on some practical considerations.
One important step is the choice of the
gauge in which to express the two-body relativistic interaction. For the exact
solution we know that the result should be gauge independent but this will not
hold for approximate solutions (remember the length and velocity forms for
dipole radiative transition probabilities).
The final result for g(1,2) of Eq. (5) reads:
|
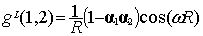
|
(8)
|
when selecting the Lorentz gauge, while the
same quantity in the Coulomb gauge is given by [12]:
|
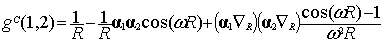
|
(9)
|
where 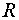 is the
interelectronic distance
is the
interelectronic distance 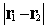 and
and 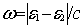 is the frequency of
the virtual exchanged photon given in terms of the single particle energies e.
is the frequency of
the virtual exchanged photon given in terms of the single particle energies e.
At the zero frequency limit Eq. (9) reduces
to the Breit interaction [13] that was first derived through second order
perturbation theory. Because of this perturbative derivation it was sometimes
argued that the Breit operator should not be included in a self-consistent
process. But, as the bound state Furry picture gives the same result, there is
no reason to exclude it from the self-consistent field if we stay at the zero
frequency limit. To go beyond would require replacing the frequency w of the virtual photon by operators.
The
expectation values of the two operators defined by Eq. (8-9) are equal for
in-shell matrix elements when a local potential is used to define the
single-particle states, but they differ for Dirac-Fock orbitals. The off-shell
contributions are already not the same even for local potential wave functions
[14] so that the choice of gauge is of practical importance. It has been shown
[15] that the Coulomb gauge is a better choice since the use of standard many-body
perturbation theory includes only the reducible part of the multiphoton
exchange (i.e. without crossing photons). The underlying justification is, that
to restore gauge invariance to leading relativistic order, the irreducible
contributions must be taken into account. As these irreducible contributions
give a non-zero contribution in the Lorentz gauge while they vanish in the
Coulomb gauge it is thus more efficient to express the interaction in the
Coulomb gauge. The same conclusion was reached by J. Sucher [16] on the grounds
that the non-pertubative use of Eq. (8) leads to incorrect energy levels
already at order a4.
4. Relativity and
atomic structure
Relativistic Hartree-Fock (also called
Dirac-Fock) calculations for atoms started to appear in the late 60's for light
atoms using basis set expansions [17], and at the beginning of the 70's by
solving the integro-differential Dirac-Fock equations by numerical methods
[18-19]. This latter approach was rapidly capable to cover the full periodic
table (see Ref. 20), and a picture rather different from the well studied
hydrogenic case started to emerge. Contrary to the single electron solution of
the Dirac equation showing mainly the mass variation with velocity, a
Dirac-Fock calculation includes the changes in the spatial charge distribution
of the electrons induced by the self-consistent field. As the charge
distribution of the inner electrons contracts towards the nucleus, the
effective charge experienced by outer electrons is reduced and they may become
less bound when compared to non-relativistic predictions. There will obviously
be an interplay between the direct relativistic correction (the mass variation)
and the indirect one (the charge redistribution) greatly dependant on the
localisation of the wave functions and whether or not they have some finite
density close to the nucleus where the local speed of the electron is high.
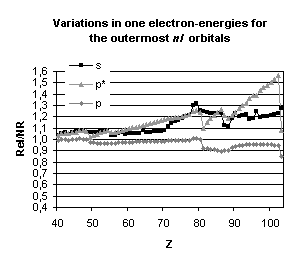
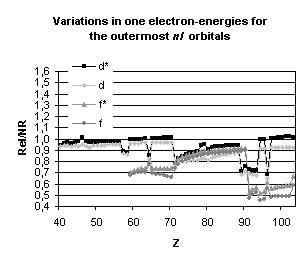
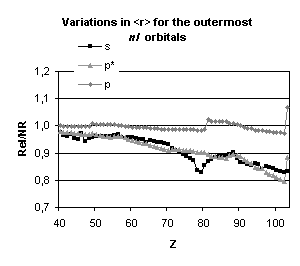
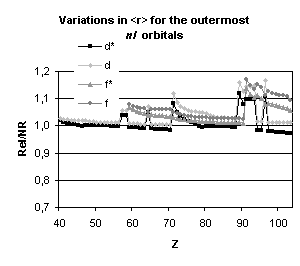
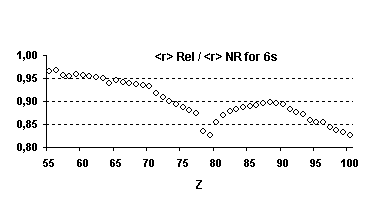
Figure 4 below illustrates the relativistic corrections to the binding energies
and mean expectation value of <r> for the outermost nl occupied
orbitals of atoms with nuclear charge greater than 40. Besides the
discontinuities observed when the principal quantum number is changing by one
unit and those due to the shell structure (for example, in the lanthanide
series, the 5d orbital is occupied only in cerium, Z=58, and in gadolinium,
Z=64) some general trends emerge:
-
orbitals with a total angular momentum
j=1/2 suffer a strong relativistic contraction as can be seen from the increase
in their binding energies and the decrease in their mean expectation value of
<r>,
-
those with j=3/2 remain essentially
unchanged until Z becomes greater than 70,
-
for high angular momenta (j=5/2 and
above) the indirect relativistic effect dominates and results in loosely bound
orbitals with radial charge densities delocalized when compared to their
non-relativistic counterparts.
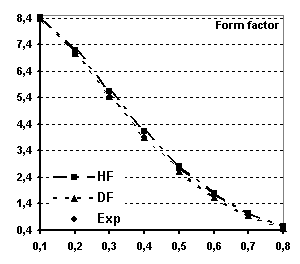
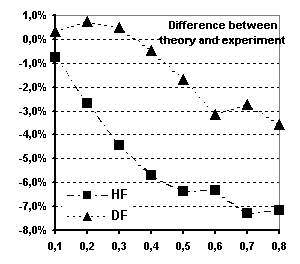
Fig 6 Spherical magnetic form factor of
Tb (see text for explanations)
We
now turn to the behaviour of electron binding energies and consider just two
examples that will provide a smooth transition to the incidence of relativistic
corrections in the prediction of chemical properties of molecules. The first
example is related to the relative binding energies of electrons with different
angular momenta. According to relativistic calculations (and in agreement with
experiment) the binding energy of a 4f5/2 electron becomes lower
than the binding energy of a 5s electron for bismuth (Z=83) and heavier atoms
while this crossover is predicted to occur at lower atomic number (Z=78) by
non-relativistic calculations. More drastic changes are observed for superheavy
atoms as in the case of lawrencium (Z=103). Extrapolation from lighter atoms of
the same column in the Periodic Table would suggest that its ground state
configuration should be 7s2 6d. But, because of the strong
stabilization of the p1/2 orbitals, it was rapidly suggested [22]
that the 7s27p1 might indeed be lower in energy. This was
confirmed by rather extensive calculations [23] including all possible
configurations obtained by distributing the three valence electrons among the
6d, 7s and 7p orbitals for the J=1/2 and 3/2 states, complemented by an
estimation of the core polarization contribution. These earlier calculations
have been more recently extended by using the accurate coupled cluster method
[24].
Accurate
predictions of electronic structure require going beyond the independent
electron picture given by the Hartree-Fock approximation and it is obvious that
correlation and relativistic corrections should be included simultaneously in a
coherent scheme. Not unexpectedly, methods that had proven their efficiency in
non-relativistic calculations started to be extended to the relativistic
domain. To give some examples:
-
the multiconfiguration method of
Froese-Fischer [25] was extended to the relativistic case [26-27],
-
the time dependant Hartree-Fock method
[28], also known as the random phase approximation, gives rise to the
relativistic random phase approximation [29],
-
the many body perturbation theory
pioneered by H. Kelly [30] also found its relativistic counterpart [31],
-
the coupled-cluster pair correlation
approach [32], like other methods, did not resist its extension to relativity
[33].
To not leave the reader with the impression
that these extensions are trivial, let us recall that a relativistic
reformulation cannot ignore the virtual creation of electron-positron pairs nor
the fact that the Breit interaction involves the exchange of transverse
photons.
For
many electron systems, QED corrections must also include many-body
contributions. For the time being only a limited number of results, besides
semi-empirical extrapolations, are available for heavy elements where a
perturbative Za approach (in terms of the electron
nucleus interaction) is irrelevant. The reason is not only that the most
precise numerical methods developed for the one-electron contributions [34]
encounter serious numerical accuracy problems for high angular momentum values
but also that, even for two-electron atoms or ions, the standard QED prescription
[35] is unable to deal with quasi-degenerate levels. Recent developments
[36-37] open new perspectives for getting accurate estimates in two-electron
systems without any restriction on the nuclear charge.
5. Going to molecules
Considering the outermost atomic orbitals,
the effects of relativistic corrections on one-electron binding energies and
the spatial distribution of the radial charge densities are illustrated by the
results displayed in Fig. 4. From the
strong dependence of these relativistic corrections upon the total angular
momentum we expect that they will not be without impact on molecular
properties.
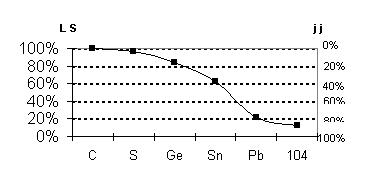
Fig 7 transition
from LS to jj coupling along the IVA column of the Periodic Table
Indeed, as the p1/2 orbitals
differ in behaviour from the p3/2 orbitals, it is obvious that the
six electrons of a p orbital will not be equivalent when hybridization is
involved to form bonding molecular orbitals including heavy atoms. As an
illustration, we display in Fig. 7 the transition from LS to jj coupling down
the Group 14 column of the Periodic Table as given by the Dirac-Fock method.
The
relative splitting between orbitals with different angular momenta is also very
sensitive to relativistic corrections. To illustrate this we consider the
outermost d and s levels in silver and gold as shown below in Fig. 8. It is
obvious that, a non-relativistic calculation predicts the valence orbitals of
the two atoms to be quite similar while a relativistic calculation shows that
the gap between the nd and ns orbitals is reduced by a factor close to two in
gold compared to silver. We know from everyday observation that silver is white
while gold is yellow, and consequently their electronic structures must show
some differences (see Ref. 38 and last chapter in this book). Beside the fact
that they differ in colour, gold and silver exhibit quite different chemical
properties. Some compounds of gold (CsAu and RbAu) are semi-conductors
instead of metals, and gold is able to form trivalent and pentavalent compounds
in contrast to copper or silver (with the exception of CuF4-
and AgF4-).
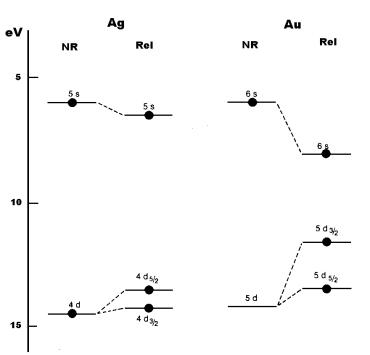
Fig 8 ns and nd
eigenvalues for silver and gold
If
we look again at the results of Fig. 4 we may expect for molecules including
heavy atoms that bond lengths obtained from relativistic calculations differ
from those predicted for the non-relativistic case. Indeed, as chemical bonding
results in a well-defined distance between the atoms that form the molecule
(equilibrium distance), this distance originates from a subtle balance between
the overlap of valence atomic orbitals in the molecule and the Coulomb
repulsion between the nuclei. Thus, if valence orbitals undergo a relativistic
contraction (like the s and p orbitals), we expect shorter bond lengths in a
relativistic calculation compared to a non-relativistic one. The opposite
effect is anticipated for high angular momentum bonding orbitals. This rather
crude point of view must be taken with some care since orbitals of quite
different angular momenta hybridise to form molecular bonds. Indeed, from
atomic results it was suggested that compounds of radium (7s2)
should have equilibrium distances lower or equal to those of barium (6s2)
compounds. Even the crudest molecular model calculations (see the one-centre
expansion section below) showed larger bond lengths for radium compounds (due
to strong d contribution) as confirmed by experiment.
All these
qualitative changes and trends can be inferred from results of atomic
calculations obtained at the beginning of the seventies of the last century, but
it remained to obtain more quantitative results. At that time all electron
calculations for molecules involving heavy atoms using relativistic four
component molecular orbitals were practically intractable even at the simple
Hartree-Fock level. Therefore, early relativistic quantum chemistry emerged
from the following various approximations:
-
stay with all the electrons in a fully
relativistic approach as given by the zero frequency limit of the Hamiltonian
in Eq. (9) but restrict to model hydride molecules in the one-centre
approximation only (see next section),
-
restrict to valence electrons only and
replace the core by a pseudopotential (see the chapter by M. Dolg in this
book),
-
go to a local density approximation
(LDA) for the exchange and correlation terms following the pioneering works of
Slater[39], and Kohn and Sham [40].
The LDA approach originated from
solid-state physics where, the Hartree-Fock approximation being less useful, it
is mandatory to take electron correlation from the beginning into account, and
this is almost always done in the framework of density functional theory. As
the non-relativistic density functional had to be changed to take relativity
into account [41], the practitioners of band calculations rapidly changed to
the Dirac equation, and as early as 1981 a rather complete picture of the
influence of relativistic effects in band structures emerged [42]. For
application to solids and molecules an efficient numerical integration scheme,
known as the discrete variational method, was developed [43], which is still
very useful [44]. The density functional method is discussed more extensively
in the chapter by Engels in this book.
5.1 Dirac-Fock one-centre method.
The Dirac-Fock
one-centre method was the first approximation used for relativistic molecular
structure calculations and is now only of historical importance. In this method
the electron-electron interaction is handled exactly and the one-electron wave
functions are four component Dirac spinors. On the other hand both the nuclear
potentials and all the one-electron orbitals are expanded about a single common
centre taken to be the position of the nucleus of the heaviest atom of the
system under consideration. Because of this expansion, the method is restricted
to hydrides XHn and even for them the expansion is only slowly
convergent. Nevertheless, experience gained with non-relativistic calculations
has shown surprisingly good results for equilibrium distances of X-H bonds and
for force constants.
To
construct the potential due to the off centre nuclei, for each of them we
choose a coordinate system with its origin at the expansion centre and the z
axis passing through the nucleus for which we expand the potential. In doing so
we obtain an expression for each of the off centre nuclei. The next step is to
rotate all these contributions to a common coordinate system which requires the
Wigner rotation matrices. The explicit results for the many symmetries applied
are published elsewhere [45] and we write the potential created by the protons
located at a distance R from the centre of expansion in the generic form:
|
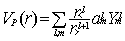
|
with r< = min (r,R)
and r> = max(r,R) while  are the usual
spherical harmonics. The value of the a coefficients is determined from
spatial symmetry of the hydride considered with only a few of them being
non-zero, so that the summation over l and m runs only over a
limited number of terms. The next step is to construct a set of one-electron
orbitals belonging to a certain irreducible representations of a double point
group. Consider the s-orbital
of a mono-hydride expanded in terms of only s and p atomic orbitals:
are the usual
spherical harmonics. The value of the a coefficients is determined from
spatial symmetry of the hydride considered with only a few of them being
non-zero, so that the summation over l and m runs only over a
limited number of terms. The next step is to construct a set of one-electron
orbitals belonging to a certain irreducible representations of a double point
group. Consider the s-orbital
of a mono-hydride expanded in terms of only s and p atomic orbitals:
with the orbitals being normalized:
This simple example is sufficient to point
out that, to be able to solve the self-consistent equations of the one-centre
method, an atomic program needs to be modified only in the following form:
-
all the atomic orbitals (s and p in
the present example) used to build a given molecular orbital must be associated
with the same eigenvalue,
-
the relative norm of the atomic
orbitals has to be optimized during the self consistent process,
-
off diagonal Lagrange multipliers must
be introduced to enforce orthogonality between core and valence orbitals even
for closed shells.
To conclude this short description of the
Dirac-Fock one-centre expansion method (a more extensive presentation can be
found in Ref. 45) we list in the table below most of the model molecular
systems computed with that method and the main conclusions drawn from these
calculations (see Table 7.3 in Ref. 2 for a full list of references to the
results summarized here).
Table 2
Hydrides studied
by the one-centre Dirac-Fock method
|
Molecules
|
Main impact of relativistic corrections
|
|
CH4 to PbH4
|
Bond length contraction and increase of force
constants
|
|
CuH, AgH and
AuH
|
Increase of the dissociation energy. Explanation of
the difference between Ag and Au.
|
|
BH to TlH
|
Decrease of the dissociation energy for TlH and
monovalency of TlH partially due to 6p spin-orbit splitting. Transition from
LS to jj coupling in bonding orbitals.
|
|
TiH4 to (104)H4
|
Small bond length expansion for TiH4 and
ZrH4.
|
|
CeH4 , ThiH4 ; UH6
,
CrH6 to (106)H6
|
5d orbital of W moves to bonding region and W-H
bonds strengthened. Further evidence for 5f participation in U-H bonds.
Contraction in actinide series found of the order of 30 pm.
|
|
MH+ and MH2 with
M = Be to Ra, Zn to Hg, Yb and No
|
Increasingly strong d contributions to the bonds
from Ca to Ra. Ra-H bonds longer than Ba-H ones. Yb-H and No-H bonds are
about the same. Explanation of the linear two coordination of Hg.
|
|
1S states of ScH to AcH, TmH, LuH and LrH
|
Trends in group 3. Lu-H and Lr-H bond lengths
comparable.
|
Table 2 includes almost all calculations done before 1980 and
illustrates the large number of systems studied under the impulse of P. Pyykkö.
Despite its obvious limitations, the one-centre method clearly demonstrated (at
least qualitatively) that relativity and chemistry of heavy elements cannot be
treated separately in contrast to what Dirac thought 50 years before (see
introduction) and as was still believed some decades later by prominent physicists:
"Modern elementary-particle physics
is founded upon the two pillars of quantum mechanics and relativity. I have
made little mention of relativity so far because, while the atom is very much a
quantum system, it is not very relativistic at all."
(Sheldon L. Glashow in his book
"Interactions", Warner, New-York, 1988)
To illustrate
that not only prominent physicists can be wrong let me correct some
interpretations given above that follow the chronological order in the
literature. From what was outlined before one may conclude that changes in the
predicted bond lengths are directly related to the relativistically induced
contraction or expansion of atomic charge distributions. This is not quite
correct as was shown by Ziegler et al. [46] using non-relativistic orbitals
while relativistic corrections to the total energy of the system were computed
by perturbation theory. In doing so, the bond length contractions obtained with
the fully relativistic one-centre method is essentially recovered and thus
appears to result more from corrections to the energy than from charge
redistribution. Nevertheless, if the relativistic contraction of atomic
orbitals and the decrease in bond lengths may be viewed as uncorrelated, they
both originate from the relativistic decrease in the kinetic energy due to the
mass-velocity correction.
5.2 Relativistic quantum chemistry.
One-centre
calculations could only provide qualitative trends of relativistic corrections
because they are restricted to few model systems. What remained was to obtain a
more detailed understanding of the interplay between relativistic, shell
structure and electron correlation effects to underline the importance of
relativity to chemistry. At the beginning of quantum relativistic calculations,
the extension of standard non-relativistic quantum chemical methods by using
one-electron wave functions expanded in basis sets to the relativistic domain
faced many difficulties in handling the unbounded Dirac operator. The
Ritz-Rayleigh variational procedure valid for semi-bound operators lead to what
is known as the variational collapse for the Dirac operator, i.e. the fact that
the total electronic energy E was diverging towards minus infinity. To avoid
this problem, boundary conditions had to be introduced into the variational
procedure (the most well known are the
kinetic balance and the non-relativistic limit of the basis spinors). The
kinetic balance condition defines the basis set for the small component from
that of the large component at the Pauli limit with a careful choice of the
contraction scheme for both components:
|
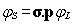
|
Furthermore large basis sets are needed for
an accurate description of the region close to the nucleus where relativistic
effects become important. Methods based on the replacement of the Dirac
operator by approximate bound operators (square of the Dirac operator, its
absolute value etc…) have not been very successful as can been understood from
the fact that they break the Lorentz invariance for fermions.
We
shall not elaborate on all the methods now used in relativistic quantum
chemistry and following chapters in this book will cover most of them rather
extensively. They range from all electron “fully” relativistic at the
Dirac-Fock level to semi-empirical methods, and from relativistic corrections
introduced perturbatively, to pseudo-potential approximations and local density
functionals. Because of the interest in molecules containing heavy elements,
ranging from catalysis to bioinorganic chemistry, the last decade brought a
large increase in the number of relativistic molecular calculations. For the
heaviest elements, say beyond mercury, most of the calculations are still
performed by using pseudo-potential or density functional approximations as
illustrated in Table 7.10 of the third volume of Ref. 2.
6. Conclusions
This short historical introduction to
relativistic electronic structure, and even more so the chapters that follow,
illustrates a very alive and active field of research whose vigour is
illustrated by the increasing number of publications in this field. Indeed, if
in 1986 a single volume published by Pyykkö [2] was sufficient to list all the
related publications on relativistic quantum theory (about 3 100) over a period of 70 years, the next 15 years
required two more volumes to hold the list of almost 8 000 new articles or
reviews devoted to this subject. Although inflation in publishing is a common
feature of all fields of research, these figures clearly show the importance to
take relativistic and QED contributions into account. The need to include
relativistic effects in quantum chemical calculations has stimulated both
conceptual and numerical developments to finally fulfil the wish of Dirac for
"approximate practical methods"
The
fact that we are now able to compute transition energies, lifetimes of excited
states, etc… with an accuracy competitive with the uncertainty of the most
precise experimental measurements is not only satisfying for the theoreticians'
ego but has also a very fundamental impact. For example, the last value for the
fine structure constant recommended by the 2000 CODATA could not have been
obtained without the measurement of the anomalous magnetic moment of the
electron at a few ppb level combined with the most accurate QED contribution
[47]. To confirm this new value (the relative change with respect to the
previous value is 7´10-8)
experiments and calculations are currently carried out to determine the 23P
fine structure splitting in atomic helium [48].
For
more complex systems, very accurate electronic structure calculations are also
useful to test the most fundamental theories of physics. Being able to compute
the parity non-conservation contribution (PNC, see chapter 9) to the hyperfine
structure [49] allows testing of quantum chromodynamics in a domain of energy not
available to high-energy physics experiments. One of the original relativistic
atomic structure programs [26], has recently been modified to handle particles
other than electrons, which made it possible to study more "exotic"
systems (i.e. systems in which one electron is replaced by a muon, a pion or a
kaon). If the "exotic" particle is a boson of spin zero this implies
replacement (for that particle) of the Dirac equation by the Klein-Gordon
equation. These new calculations, in connection with highly accurate X-ray
measurements of trapped pionic atoms, should lead to a substantial increase in
the precision of the pion mass [50]. A higher accuracy in the value of the pion
mass will result in a more reliable upper limit for the mass of the muonic
neutrino, which is of prime importance in cosmology (dark matter of the
universe). These last two examples demonstrate that we are now moving way
beyond atomic and molecular properties.
References
[1]
P.A.M
Dirac, Proc. Roy. Soc. A 117 (1928), 610
[2]
For a
complete list of references see P. Pyykkö, Relativistic theory of atoms and
molecules, Springer Verlag, 1986 (I), 1993 (II) and 2000 (III)
[3]
W. Pauli and
V. Weisskopf, Helv. Phys.
Acta 7 (1934), 709
[4]
W. E.
Jr Lamb and R.C. Retherford, Phys. Rev. 72 (1947), 241
[5]
T.
Stöhlker et al., Phys. Rev. Letters 85 (2000), 3109
[6]
J.
Sucher, Phys. Rev. A 22 (1980), 348
[7]
M. H.
Mittleman, Phys. Rev. A 24 (1981), 1167
[8]
G. E.
Brown and D. G. Ravenhall, Proc. Roy. Soc. London A 208 (1951), 552
[9]
I.P.
Grant in “Relativistic effects in atoms, molecules and solids” (ed. G.L.
Malli), Plenum Press, New-York, 1983
[10]
K.G.
Dyall, I.P. Grant and S. Wilson, J. Phys. B: At. Mol. Phys. 17 (1984) 493
[11]
W.H.
Furry, Phys. Rev. 81 (1951) 115
[12]
V.B.
Berestetskii, E.M. Lifshitz and L.P. Pitaevskii, Relativistic Quantum Theory,
Oxford Pergamon, 1971
[13]
G. Breit,
Phys. Rev. 53 (1938),
153
[14]
O.
Gorceix and P. Indelicato, Phys. Rev. A 37 (1988), 1087
[15]
I.
Lindgren, J. Phys. B: At. Mol. Phys. 23 (1990) 1085
[16]
J.
Sucher, J. Phys. B: At. Mol. Phys. 21 (1988) L585
[17]
Y.K.
Kim, Phys. Rev. 154 (1967), 17
[18]
J.B. Mann
and J.T. Waber, J. Chem. Phys.
53 (1970)
[19]
J.P.
Desclaux, D.F. Mayers and F. O'Brien J.
Phys. B 4 (1971) 296
[20]
J.P.
Desclaux, At. Dat. and Nuc. Dat. Tables 12 (1973) 311
[21]
G.H.
Lander, T.O. Brun, J.P. Desclaux and A.J. Freeman, Phys. Rev. B 8 (1973), 3237
[22]
L.
Brewer, J. Opt. Soc., 61 (1971) 1101
[23]
J.P.
Desclaux and B. Fricke, J. Physique 41 (1980) 943
[24]
E.
Eliav, U. Kaldor and Y. Ishikawa, Phys. Rev. A 52 (1995) 291
[25]
C.
Froese-Fisher, "The Hartree-Fock Method for atoms" Wiley, New-York,
1977
[26]
J.P. Desclaux,
Computer Phys. Commun. 9 (1975) 31
[27]
I.P. Grant, B.J.
McKenzie, P.H. Norrington, D.F. Mayers and N.C. Pyper, Computer Phys. Commun.
21 (1980) 233
[28]
M. Ya. Amusia and N.A. Cheperekov, Case
Stud. At. Phys. 5 (1975) 47
[29]
W.R.
Johnson and C.D. Lin, Phys. Rev. A 20 (1979) 964
[30]
H.P.
Kelly, Phys. Rev. 131 (1963) 684
[31]
W.R.
Johnson and J. Sapirstein, Phys. Rev. Lett. 57 (1986) 1126
[32]
I.
Lindgren and J. Morison, "Atomic many-body theory" Springer-Verlag,
1982 and 1986
[33]
E.
Lindroth, Phys. Rev. A 37 (1988) 316
[34]
P.J.
Mohr, Ann. Phys. (NY) 88 (1974) 25 and 52
[35]
J. Sucher,
Phys. Rev.107 (1957)
1448
[36]
V. A. Yerokhin, A. N. Artemyev, T.
Beier, V. M. Shabaev and G. Soff, J. Phys. B: At. Mol. Phys.
31 (1998) L691
[37]
I. Lindgren,
Mol. Phys. 98 (2000) 1159
[38]
N. E. Christensen and B.O. Seraphin,
Phys. Rev. B 4 (1971) 3321
[39]
J.C.
Slater, Phys. Rev. 81 (1951) 385
[40]
W.
Kohn and L.J. Sham, Phys. Rev. 140A (1965) 1133
[41]
A.H.
McDonald and S.H. Vosko, J. Phys. C 12 (1979) 2977
[42]
D.D.
Koelling and A.H. MacDonald in “Relativistic effects in atoms, molecules and
solids” (ed. G.L. Malli), Plenum Press, New-York, 1983
[43]
D.E.
Ellis and G.S. Painter, Phys. Rev. B2
(1970) 2887
[44]
B. Fricke et al., Adv. Quantum Chem. 29 (1997) 109
[45]
J.P.
Desclaux in “Relativistic effects in atoms, molecules and solids” (ed. G.L.
Malli), Plenum Press, New-York, 1983
[46]
T.
Ziegler, J.G. Snijders and E.J. Baerends, Chem. Phys. Lett. 75 (1980) 1
[47]
P.J.
Mohr and B.N. Taylor, Rev. Mod. Phys 72 (2000) 351
[48]
M.C.
George, L.D. Lombardi and E.A. Hessels, Phys. Rev. Lett. 87 (2001) 3002
[49]
W.R.
Johnson, J. Sapirstein and S.A. Blundell, Phys. Scr. T46 (1993) 184
[50]
G.L. Borchert et al., Hyperfine Interactions
132 (2001) 195
![]() are matrices that
fulfil the commutation rule
are matrices that
fulfil the commutation rule![]() where
where ![]() is the metric tensor
is the metric tensor![]() is the four-vector
is the four-vector![]()
![]() and energy E
of the particle and of the vector (
and energy E
of the particle and of the vector (![]() ) and scalar (
) and scalar (![]() ) potentials of the external electromagnetic field. As for
all the remaining sections of this chapter we shall consider only time
independent scalar external fields, we rewrite Eq. (1) in the usual form:
) potentials of the external electromagnetic field. As for
all the remaining sections of this chapter we shall consider only time
independent scalar external fields, we rewrite Eq. (1) in the usual form:![]() . In this system the speed of light c » 137 is the inverse of the fine structure constant. For the (4x4)
Dirac matrices a
and b we adopt the conventional
representation that is useful when considering the non-relativistic limit of
the Dirac equation. In this standard representation the components of a are expressed in terms of the
(2x2) Pauli matrices and b is taken to be diagonal, explicitly:
. In this system the speed of light c » 137 is the inverse of the fine structure constant. For the (4x4)
Dirac matrices a
and b we adopt the conventional
representation that is useful when considering the non-relativistic limit of
the Dirac equation. In this standard representation the components of a are expressed in terms of the
(2x2) Pauli matrices and b is taken to be diagonal, explicitly: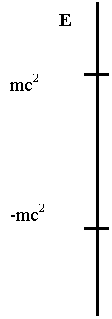



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()