INPUT DATA FOR RELATIVISTIC ATOMIC PROGRAM
MCDFGME V 2005.10
J.P. Desclaux*
15 Chemin du Billery, 38360 SASSENAGE France
P. Indelicato†
Laboratoire Kastler Brossel,
CNRS, École Normale Supérieure et Université Pierre et Marie Curie
Case 74, 4 Place Jussieu, 75252 Paris CEDEX 05
Last revision: August 8, 2005
*e-mail : jean-paul.desclaux@wanadoo.fr
†e-mail : paul@spectro.jussieu.fr
Contents
Chapter 1
INTRODUCTION
This package calculates a number of atomic quantities, taking fully into account relativistic effects. In the
current version, the code is able to:
- build the eigenstates of the total angular momentum J2,
- calculate the angular coefficients for energy expression (including Gaunt, Breit and higher
order retardation),
- solve the multiconfiguration Dirac-Fock equations (with all orbitals relaxed) including various
contributions self-consistently (Coulomb, Breit, vacuum polarization),
- include, besides electrons, several exotic particles, including bosons,
- correct the total energy for QED contributions,
- compute
total energy of a given state either at the single configuration or multiconfiguration level,
radiative transition probabilities,
Auger transition probabilities,
photoionization cross sections,
hyperfine structure constants,
Landé factor,
Born electron impact excitation cross section,
Stark effet,
parity non-conserving amplitude,
magnetic part of the g - 2 correction for antiprotons,
scalar product of wave functions.
Shiff moment
Overlaps of orbitals between a n-electron and a n - 1-electron state for Shake-off
calculations
For each set of input data, variables to be read are listed either in upper or lower case with the following
conventions :
- variables listed in upper case must be given a value.
- for variables listed in lower case default values are automatically assigned if no value is given
as input.
- Default values are given in parentheses and underlined after the definition of the variables.
- Lines begining with the character # in the first column are treated as comments.
All input data are read in free format using the a proprietary set of subroutines. The conventions used are
the following :
- Input stream may include an arbitrary number of data sets, one for each case to be calculated.
A data set is composed of a certain number of files each of them divided into an arbitrary
number of records.
- A file is defined as an arbitrary number of input lines followed by a line with end as its first
3 characters.
- A record is defined as an arbitrary number of input data. A record may extend over an
arbitrary number of lines and more than one record may be on the same line. The character
“:” after at least one blank may be used to interrupt data list of a record and let the program
assign default values to the rest of the data in the record.
- An input line is a set of 72 characters followed by a carriage return.
- The first 4 characters of each input line are considered as an identifier that can be used to
identify a set of input data.
- An input value is defined as a string of characters without blanks.
- Strings are separated by at least one blank.
- An input value and its optional identifier (see below) must be on the same line.
For convenience each input value can be labeled with an identifier followed by the character “=”. Both the
identifier and the character “=” are considered as comments and are thus ignored (It is not list-directed
inputs!).
Valid input data are : strings of characters (case insensitive), integers or real numbers.
The atomic states are defined as a superposition of electronic configurations each of which is defined as a
list of orbitals with their occupation numbers. These configurations are given, as input data, in
LS coupling and the program will generate all the jj configurations arising from a given LS
configuration.
Note that:
- the configurations given as input data in LS coupling use 1s, 2s, 2p and so on as labels.
- the jj configurations generated by the program use 1s, 2s, 2p*, 2p and so on as labels. The
* denotes j=l-1/2, while no * stands for the j=l+1/2 .
- when a certain number of orbitals with the same occupation are common to all configurations,
they can be given only once at the beginning of the definition of the first configuration as a
record with CORE in the first 4 columns if the calculation involve definition of an initial and
a final level, the CORE is common to both of them). Also if some or all of these core orbitals
make up a rare gas configuration, it is sufficient to give the symbol of the rare gas to generate
the full set of orbitals. Valid symbols are: Ne, Ar, Kr, Xe and Rn.
- orbitals of identical labels can be distinguished using an extra number. For example 2p1]
will be treated by the code as different from 2p, while 2p0] and 2p are equivalent. Orbitals
with j=l-1/2 will be noted 2p1]* for example. If l is too large to use a letter (the letters valid
in the code are: s, p, d, f, g, h, i, k, l, m, n, o, q, r, t, u, v, w, x, y, z for l=0 to l=20) one
can give the orbital in the form xxSyy/ or xxSyy[n if one needs an extra label to distinguish
orbitals with same quantum numbers. xx is the principal quantum number and yy the l value.
S must be + in ls coupling. For example 40+39/ is an orbital with n=40 and l=39. 40+39[1/
or 40+39[1] are also valid orbital labels.
As examples of using the CORE keyword, input for silicon will read:
core Ne 3s2
cf 1 3p2 :
end
|
while the data for Be 1s2 2s2 + 1s2 2p2 can be given as:
core 1s2
cf 1 2s2 :
cf 2 2p2 :
end
|
FILES USED
The first file used by the program is one that defines Fortran unit numbers for inputs and output
and the generic names for all other files needed by the program. This file must be named
mdfgme.dat.
Other file names are labeled according to the following convention : for each Fortran file with number nn,
the associated name will be the generic name appended with .fnn. As an example assume that the given
generic name was testmcdgme, then the input file associated with Fortran unit number 5 must be
named testmcdfgme.f05, and testmcdfgme.f06 will the name of the output file associated with Fortan
unit number 6 and so on.
Chapter 2
Input data to be provided in the mdfgme.dat file
2.1 Fortran file numbers: Item 1
-
iread:
- fortran file number to read the next sets of input data. (5)
-
iwri:
- fortran file number for standard outputs. (6)
-
ipun:
- fortran file number to save formatted outputs. (7). This file contains the summary of
transition probability, hyperfine corrections, Auger and Photoionization cross-section, Landé
g-factors, in a comma-separated list format to import in standard spreadsheet programs. It
contain level energy, configurations, label, eigenvalue number... for each state.
-
iba:
- fortran file number for the energy expression. (8)
-
ibb:
- fortran file number to read wave functions in binary form. 9)
-
ibc:
- fortran file number to write wave functions in binary form. (9)
-
nblipa:
- number of output lines per page. (75)
2.2 Generic name of the files: Item 2
-
NAME:
- a string of 36 characters or less.
As was pointed out above this string will be appended with .fnn for all the various files used,
where the two digits nn is the Fortran unit number. Furthermore, for the energy expression,
each case to be run is associated with one or two specific file(s) depending upon the fact that
one or two state(s) is (are) involved. The name is then obtained from the generic name by
using for the 6 most rightmost characters the 3 identification characters of the case under
consideration (see the definition of the title line below) followed by _01 for the first state and
_02 for the second state if any. For the given example of input data the file(s) for the energy
expression will be given the name(s) testmcdfgmeABC_01.f08 and testmcdfgmeABC_02.f08
if ”ABC” are the 3 characters used to identify the case being runned (see 3.1.1).
2.3 Total CPU time: Item 3
-
ttot:
- maximum allowed overall running time for the job in seconds, i.e. the execution will stop if
the CPU time used becomes greater than ttot. A value lower or equal to zero dsables this
feature. (0)
Chapter 3
Input data to be provided in the second input file
This second input data file (with name testmcdfgme.f05 within the present illustration) includes data for
each case to be runned. The data for each case are divided into three subsets: the first one deals with the
data independant of the states (initial and final when two are involved). The second set defines the
configuration(s) involved while the third set includes data specific to each state and thus must be given
twice when two states are involved.
3.1 Data common to both states
3.1.1 Title: Item 4
-
ITITLE:
- title line with one asterisk as its first character and a maximum of 79 characters, the
first 3 are taken as the identification of the case being run (they are used to build the name
of the energy expression file(s), as described above).
3.1.2 Optional outputs: Item 5
For debugging purpose, names of programs in which extra output is requested, followed by a keyword
describing the amount of debugging requested (min med max). (none)
Any subroutine or function name is valid provided debug options have been implanted. For the pesent
version of the code, examples of routines inluding this option are:
-
scfmdf :
- more extensive output during the self-consistent field process.
-
hdimdf :
- more extensive output during the diagonalization of the energy matrix.
-
sdispl :
- more extensive output during solution of the inhomogeneous Dirac equation by a spline
+ projector method.
-
maelam :
- more extensive output during evaluation of one-electron operator angular coefficients
(no relaxation of orbital or diagonal cases)
-
menoam :
- more extensive output during evaluation of one-electron operator angular coefficients
(full SCF for all orbitals of the initial and final states, so that the orbitals of the two states
are not assumed to be orthogonal)
-
tranam_det :
- more extensive output during evaluation of one-electron operator (off-diagonal
case)
-
operam_det :
- more extensive output during evaluation of one-electron operator (diagonal case).
-
coevam :
- more extensive output during actual calculation of angular integrals.
-
emngme :
- more extensive output during transition probabilities evaluation.
-
hfsgme :
- more extensive output during hyperfine matrix elements evaluation.
-
pncgme :
- more extensive output during parity-non conserving amplitudes evaluation.
-
alloc :
- keep track of the dynamic allocation of arrays in the program (note that there is no
subroutine or function with that name)
-
podmdf :
- Shows direct potential contributions for Coulomb (in max. only)
-
poemdf :
- Shows exchange potential contributions for Coulomb (in max. only)
3.1.3 Speed of light: Item 6
-
MOD_LIGHTSPEED :
- must be y or n . If y speed of light is multiplied by cmux
-
- Only if mod_lightspeed is y:
-
CMUX :
- factor to multiply speed of light.
3.1.4 Atomic number: Item 7
-
NZ:
- atomic number.
3.1.5 Type of calculation and energy expression: Item 8
-
KEYWORD :
- keyword for expectation value of the energy to optimize, options available are:
mdf for full multiconfiguration.
eal for extended average energy level.
rci for relativistic interaction of configuration.
Only if KEYWORD is mdf or rci
-
DO_ENERGY :
- option to compute or not expectation value of the total energy. Must be y or
n .
-
- If option is n the energy expectation value is assumed to have been already computed and saved
in a file.
-
KEEP_ENER :
- option to keep or not the file with the expectation value of the total energy.
Must be y or n .
-
BINARY_ENER :
- the file with the expectation value of the total energy will be in binary form
if this option is y and in formatted form otherwise.
-
DO_SCF :
- option to perform or not the self-consistent field process. Must be y or n .
-
- Only if KEYWORD is rci
-
MODRCI :
- option to define how RCI Dirac-wave functions will be generated, must be y or n . If
n hydrogen-like, Thomas-Fermi or wave function read on file are to be used. If y the code will
solve the Dirac-Fock equation using BSpline for each orbital symmetry given in a list and use
the complete set thus generated in the RCI process. This complete set will be orthogonalized
to all wave functions generated by other methods. Positive continuum orbitals will be used.
3.1.6 Breit interaction: Item 9
-
KEYWORD :
- option for Breit interaction.
neglect to omit Breit interaction.
average to include Breit interaction at the average level only.
full to include exact contribution of the Breit interaction.
-
- Only if KEYWORD is not neglect
-
MAG_SCF :
- must be y or n : y if magnetic part of the Breit interaction is to be included in the
self-consistent process. If n it will be added as a first order correction after self-conistency
has been reached.
-
- Only if MAG_SCF is y
-
RET_SCF :
- must be y or n : y if retardation part of the Breit interaction is to be included in
the self-consistent process. If n it will be added as a first order correction after self-conistency
has been reached.
-
- Only if either MAG_SCF or RET_SCF is n
-
DIAG_AFTERSCF :
- must be y or n : y if a diagonalization with the complete (magnetic +
retardation) Breit interaction is to be done after self-conistency has been reached.
-
- Only if DIAG_AFTERSCF is y
-
KEEP_SCFCOEFF :
- must be y or n : y to keep the configuration weights as given by the
SCF process, n to use those from the above diagonalization for forthcoming calculations.
3.1.7 Vacuum polarization: Item 10
-
VACPOL_SCF :
- option to include or not vacuum polarization in the self-consistent process.
Must be y or n . If y , Uëhling potential is included in the Dirac-Equation. This include
diagrams with several vacuum-polarization loop The one with two-loop enter at the same
order as the Källén and Sabry contribution.
3.1.8 Calculation to be done: Item 11
Note that calculations in mode EAL are only compatible with keyword energy, as all the
others require a definite angular momentum.
-
KEYWORD :
- keyword for the type of calculation (only the first 4 characters are meaningful):
energy for a single mcdf calculation of the energy of a set of configurations
lande for a single mcdf calculation of the energy of a set of configurations followed by
the calculation of the Landé factor.
electric for mcdf calculations of the energy of two sets of configurations and
computation of the electric transtion rate between them.
magnetic for mcdf calculations of the energy of two sets of configurations and
computation of the magnetic transtion rate between them.
radiative for mcdf calculations of the energy of two sets of configurations followed by
the calculation of all the allowed electric and magnetic transtion rates between them.
born for mcdf calculations of the energy of two sets of configurations and computation
of the electron impact Born cross section between them.
hyperfine for hyperfine matrix element calculations.
pncamplitude for parity non-conserving amplitude.
stark for Stark matrix elements.
schiff for Schiff matrix elements.
scalar for scalar product of two wavefunctions to test Orthogonality.
gm2pbar to calculate the Magnetic part of the g - 2 correction for antiprotons. The
electric part which is only diagonal is calculated directly during the mcdf phase.
photoionization to calculate photionization cross sections
auger to calculate Auger transition rates
shakeoff to calculate overlaps of orbitals between a n-electron and a n-1-electron state
for Shake-off calculations
Depending upon the type of calculation selected, extra input data are needed as described
below
-
If KEYWORD is electric or magnetic:
-
MULPOL: multipole order of the transition. Can be any positive integer
ITEM 12 defined in the next subsection.
-
If KEYWORD is radiative:
-
ITEM 12 defined in the next subsection.
-
If KEYWORD is born:
-
ITEM 12 defined in the next subsection.
-
If KEYWORD is hyperfine:
-
MULPOL: must be 1 for magnetic dipole or 2 for electric quadrupole
INUC: the nuclear spin (I) multiplied by 2. The code will calculate the matrix element
for all possible values of F = J + I
GNUC: nuclear magnetic moment in nuclear magneton for mulpol=1 or nuclear
quadrupole moment (in barns) for mulpol=2
DIAG: Must be y if matrix element is diagonal or n if an off-diagonal matrix element
is computed. Note that if one choose y then only one state must be given.
-
If KEYWORD is stark:
-
ITEM 12 defined in the next subsection.
-
If KEYWORD is schiff:
-
ITEM 12 defined in the next subsection.
-
If KEYWORD is shakeoff:
-
ITEM 13 defined in the next subsection.
-
If KEYWORD is gm2pbar:
-
INUC: the nuclear spin (I) multiplied by 2. The code will calculate the matrix element
for all possible values of F = J + I
GNUC: nuclear magnetic moment in nuclear magneton for mulpol=1 or nuclear
quadrupole moment (in barns) for mulpol=2
DIAG: Must be y if matrix element is diagonal or n if an off-diagonal matrix element
is computed. Note that if one choose y then only one state must be given.
-
If KEYWORD is photionization:
-
EN_PHOTON: photon energy
ENERGY_UNIT: keyword to define the unit of energy (for available keyword to
define the unit of energy see Item 12)
ITEM 12 defined in the next subsection.
-
If KEYWORD is auger:
-
ITEM 12 defined in the next subsection.
-
If KEYWORD is 2photon:
-
IPOL1: a two character string to provide type of transition and multipole value like E1
or M2 for the first photon
IPOL2: a two character string to provide type of transition and multipole value like E1
or M2 for the second photon
ITEM 12 defined in the next subsection.
3.1.9 Transition energy: Item 12
The following data define the value of the transition energy used to compute the transition
probability.
-
USE_MCDFENER:
- must be y or n. If y the program will use computed energies to define the
transition energy. Otherwise an energy value has to be provided.
The following two input data are to be given only if use_mcdfener=n
-
ETRANS:
- Transition energy in unit defined by next data keyword
-
ENERGY_UNIT:
- unit of energy for transition energy etrans
cm for cm-1.
ev for electron volts.
au for atomic units.
mh for megahertz.
nm for nanometers.
an for Angstroems.
The following data must be providede only for the options electric and magnetic
-
SUB_OFFSET:
- must be y or n. If y a matrix element provided as the next item is subtracted
from the total transition matrix element. This is useful when a non-relativistic offset has to
be removed from the matrix element obtained in a relativistic calculation ib order to recover
the non-relativistic limit.
Only if sub_offset=y
-
ACCINF:
- Matrix element to be subtracted from the total transition matrix element.
3.1.10 Overlaps between initial and final states: Item 13
This input data is needed only for calculations involving two states.
-
OPT_RELAX :
- must be y or n. If y the program take into account lack of orthogonality between
the orbitals of the initial and final states. Do not use OPT_RELAX=n if you have optimized
initial and final wave function independently.
3.1.11 Retardation in Lorentz gauge: Item 14
-
RET_LORENTZ :
- must be y or n. If y full retardation correction in Coulomb and Lorentz
gauges are calculated including frequency dependent part.
**** This will almost double CPU time. Furthermore must be used only for single
configuration otherwise meaningless results may be produced. ****
3.1.12 Vacuum polarization due to electrons: Item 15
-
OPT_QEDEL :
- option to calculate vacuum polarization induced by bound electrons. y or n. If
y compute this contribution or do not compute if n.
-
ilams :
- distance from the origin to integrate charge density for self-energy screening, in 1/100
Compton wavelength. (30)
3.1.13 Option to modify tabulation mesh: Item 16
This option allows to modify the mesh grid onto which the wave functions are tabulated
-
MOD_MESH :
- must be y or n. If n standard options will be used.
-
- Only if MOD_MESH is y:
-
H :
- mesh step in the variable t defined as t = ln(r/r1) + ar. (0.05)
-
r(1) :
- first tabulation point multiplied by the nuclear charge NZ and the mass of the heaviest
particle. (0.01)
-
amesh :
- mesh step in the linear region, i.e. value of a in the above definition of t. (0.01)
-
nb-vp-int :
- Number of Gauss-Legendre points used in the integration of vacuum polarization
between 0 and r(1) (30)
3.1.14 Option to include a non-electron particle: Item 17
-
EXOTIC_PART :
- must be y or n. If y one exotic particle will be present. This particle will be
designed by an @ in the label as in, e.g., (1s@]). In that case, there must obviously be one
and only one such label in each configuration.
-
- Only if EXOTIC_PART is y:
-
KEYWORD :
- exotic particle name:
muon for a muon (spin 1/2 lepton)
pbar for an antiproton (spin 1/2 baryon)
pion for a pion (spin 0 meson)
kaon for a kaon (spin 0 meson)
sigma for a sigma (spin 1/2 baryon)
tstf for a test particle of mass 1 (as the electron) and spin 1/2
tstb for a test particle of mass 1 (as the electron) and spin 0 the last two are used for
debugging purposes.
3.1.15 Option to modify nuclear parameters: Item 18
This option allows to modify the parameters of the nucleus.
-
MOD_NUC :
- must be y or n. If option is n calculation is done using standard atomic masses and
with a uniform nuclear charge distribution with radius as given in NUCPOT for Z <= 45.
For Z > 45, Fermi distribution is used.
-
- Only if MOD_NUC is y:
-
A :
- Number of nucleon (used to select the mass of the isotope from internal table and to eventually
modify the nuclear radius). If A< 0 the internal value is used. If A> 400 A is set to infinity,
but internal RMS radius and isotope number are used. If a=0, allow to use an exotic nucleus
-
- Only if a=0
-
NUCDEF:
- type of exotic nucleus: positron, muon, pion are accepted. Set rms to 0 for positron
and muon, and to pion form factor for pion. fert is set to 0.
-
ferc :
- RMS nuclear radius in Fermi. (internal value for most abundant isotope)
-
fert :
- thickness parameter for the Fermi charge distribution of the protons.
(0. for Z < 45, 2.3 Fm for Z > 45)
-
nuc :
- index of the nuclear radius (1 if FERC=0. and max(NUC,41) otherwise)
For the nucleus a point charge is used when FERC is < 0 and a finite one when FERC is > 0. For a finite
charge distribution, a uniform charge inside a sphere of radius FERC is used if FERT is < 0 and otherwise
a Fermi distribution written as:
Ct/(1. + exp((r - FERC) * (4ln3)/FERT))
Ct
being a normalization constant.
3.2 Definition of the states
3.2.1 Number of electrons: Item 19
-
NBELI:
- number of electrons in initial state
-
- Only if this case involves two states
-
NBELF:
- number of electrons in final state
3.2.2 List of configurations: Item 20
As stated previously the configuraions are define in terms of LS configurations and the program will
generate internally all the associated jj configurations. Furthermore the list of configurations may be given
explicitly or generated internally as all double and single excitations starting from a ”reference”
configuration.
-
DEF_CONFIG :
- a keyword to define how the list of configurations should be handled. Two
keywords are valid data:
given if the configurations are given explicitly.
build if the configurations have to be build automatically from a reference configuration
(all single and double excitations are constructed). The code will create all single and double
excitations for all occupied orbitals between a lower one (which must be an occupied orbital)
and an upper one.
lists if the configurations have to be build automatically from a reference configuration.
In this case an explicit list of occupied orbitals to be excited, and a list of orbitals in which
to excite to must be provided.
-
- If DEF_CONFIG was assigned the keyword given
-
LIST
- of configurations, each set followed by “:”.
-
A line
- with end as the first 3 characters.
-
- If DEF_CONFIG was assigned the keyword build
-
DEFINITION
- of the reference configuration, followed by “:”.
-
A line
- with end as the first 3 characters.
-
LABORB_DEB
- label of the lowest orbital from which excitations will be build.
-
LABORB_FIN
- label of the highest orbital to which excitations will occur.
Notice that non closed-shell orbitals of the reference configuration will be considered as
available for excitations if their quantum numbers is in the range defined by laborb_deb and
laborb_fin.
-
- If DEF_CONFIG was assigned the keyword lists
-
DEFINITION
- of the reference configuration, followed by “:”.
-
A line
- with end as the first 3 characters.
-
list
- of occupied orbitals to be excited followed by “:”.
-
A line
- with end as the first 3 characters.
-
list
- of occupied or new orbitals to which excitations will occur followed by “:”. For the occupied
orbitals, the list should obviously not involve orbitals associated to a closed shell.
-
A line
- with end as the first 3 characters.
3.2.3 Brillouin excitations and extra configuration: Item 21
The next 4 sets of data have to be read only if DEF_CONFIG was assigned the keyword build or
lists
-
BRILLOUIN
- option (must be y or n) to include or not single excitations of the Brillouin type
(n
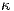
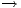 n'
n'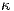 ). IF y Brillouin excitation will be included, but convergence then may be very
difficult.
). IF y Brillouin excitation will be included, but convergence then may be very
difficult.
-
EXTRACONF
- option (must be y or n). If y one can provide configurations not in the
automatically generated list (e.g., triple excitations)
-
- Only if EXTRACONF is y
-
DEFINITION
- of each extra configuration, followed by “:”.
-
A line
- with end as the first 3 characters.
-
Note:
- as stated in the introduction the defintion of the configuration(s) can begin with one or
more record(s) identified by CORE to define all the orbitals common to all configurations
for the first and second state if any.
-
2 states:
- If the case under consideration involves two states, the above input data have to be
repeated for the second state without the CORE definition, if any, since from above it is
assumed to be shared by the two states
3.2.4 Total angular momenta: Item 22
-
JJTOT :
- twice the value of the total angular momentum J.
-
mjjtot :
- twice the projection M = Jz of the total angular momentum J. (JJTOT)
-
2 states:
- If the case under consideration involves two states, the above data are for the first state,
same data must also be given for the second state
3.2.5 Negative continuum: Item 23
-
IFLAGP :
- option to project out on the positive energy subspace when using BSplines to solve
the inhomogeneous Dirac-Fock equation for correlation orbitals, must be y or n . If y the
negative continuum is excluded by keeping only the positive energy solutions while for n both
negative and positive solutions are kept. As a general guide, y should be used when the energy
is the primary aim of the calculation and n when one-electron operators are the main concern
(transition rate, hyperfine structure, or pnc amplitude).
3.2.6 Particle finite size: Item 24
To be given only if the calculation involves a non-electron particle and if this paticle is either an
antiproton, a pion or a kaon.
-
IPFSSC :
- must be y or n : Correction due to particle size is treated self-consistently if y and in
perturbation otherwise. It is important to use y if g - 2 correction for antiproton is to be
evaluated for j = 1/2 states
3.3 Data for each state
3.3.1 Define state to which convergence is requested Item 25
-
NEIGV :
- the order of the eigenvalue towards which convergence is to be achieved. If positive
it will be the NEIGV-th eigenvalue (the first being the lowest). If negative it will be the
eigenvalue having the |NEIGV|-th configuration as its largest component. If = 0 convergence
will be towards a given LSJ level or all eigenvalues will be explored depending upon the
value of the next input data. Note that the value of NEIGV is irrelevant in EAL
mode but the zero value is not permitted since reading next input data would be
meaningless.
-
LSJLEVEL :
- to be given only if NEIGV = 0
either as the definition of an LSJ level in the form XL#n where X=2S+1 (S being the spin
value), L the total angular momentum and n an energy ordering (n=1 will correspond to
the lowest energy if the ground configuration was defined first in the configuration list) for
converge to the eigenstate having the largest weight of the given LSJ level
or as ALL if all eigenvalues have to be calculated self-consistenly. For a two-state case, all
possible combinations between initial and final states will be obtained if ALL is set for both
states.
3.3.2 Initial configuration weights and printout of energy expression Item 26
-
ICMUL :
- initial mixing coefficients between the configurations are read (see Item 35) as input
data if ICMUL is not zero. If some wave functions are read from file, the mixing coefficients
corresponding to the configurations already calculated are read too. Furthermore if ICMUL<
0, the weights are frozen to their initial values during all the SCF process. (0)
If ICMUL> 3 Item 36 consist of two values: a replacement threshold and a replacement value.
After first diagonalization all mixing coefficient with value lower than threshold are replaced.
Signs are kept.
-
iprt_energ :
- energy expression is written on the standard output if IPRT_ENERG is not 0. (0)
3.3.3 Mainly common data for all orbitals Item 27
-
NORBSC :
- define orbitals to be made self-consistent. If equal to 0 all orbitals are made self
consistent. If < 0 all orbitals are frozen. If > 0 some orbitals (list to be given below as Item
31) are frozen.
-
ndep :
- default option for initial orbitals. (1)
< 2 calculated with the Thomas Fermi potential.
= 2 hydrogenic.
= 3 read from a binary file.
=4 internal use only! Use BSpline basis to generate RCI orbitals
-
nlec :
- record number to read initial orbitals from a binary file. (0)
-
nec :
- record number to write orbitals on a binary file. (0)
-
ifcwf :
- convergence acceleration factors are kept fixed if IFCWF is not 0. (0)
-
nes :
- number of trials to adjust one-electron energies when solving the Dirac equation. (40)
-
iprt_fgr :
- after self consistency has been achieved, radial integrals for the energy are printed only
if IPRT_FGR is not 0. (0)
-
idfbeg :
- deferred correction is used from the beginning of the SCF process if IDFBEG=0.
Otherwise it is used only after the accuracy in the wavefunctions is lower than 0.01%. (0)
3.3.4 Number of SCF cycles Item 28
-
NSTEP :
- number of cycles in the SCF process (a cycle is defined by the various parameters
described in the next Item before a diagonalization is performed for a multiconfiguration
calculation). If lower than 1 input is replaced by (1) for a single ((5) for a multi) configuration
calculation.
3.3.5 SCF cycle parameters Item 29
Only if NSTEP is greater then 0: for each cycle N (N=1 to NSTEP).
-
ISCPAR(1,.) :
- exchange potential is included only if not 0. Furthermore, Schmidt
orthogonalization is used if < 0. (1)
-
ISCPAR(2,.) :
- if 0, omit off-diagonal Lagrange multipliers. (1)
-
ISCPAR(3,.) :
- number of iterations divided by number of orbitals. (30)
-
AZPRY(1,.) :
- nuclear charge. (=NZ)
-
AZPRY(2,.) :
- accuracy to be reached for the radial functions. (10**(NSTEP-6-N))
-
ACCF(1,.) :
- mixing coefficient of the eigenvectors between 2 iterations. (1.)
-
ACCF(2,.) :
- fraction of Coulomb electron exchange to be included. (1.)
-
ACCF(3,.) :
- fraction of the Breit contribution to the electron exchange to be included (usefull
only when Breit is included in the SCF). (1.)
3.3.6 Accuracy parameters Item 30
-
OPTION
- to use regularization when computing magnetic integrals must be y or n.
-
OPTION
- to modify accuracy criteria must be y or n.
-
- Only if option is y:
-
teste :
- relative accuracy to be obtained for one-electron energies. (0.000005)
-
rap :
- defines the accuracy to which the small component has to be matched when solving the
Dirac equation as the ratio AZPRY(2,.)/RAP. (100.)
3.3.7 List of frozen orbitals Item 31
Only if NORBSC > 0: labels of the frozen orbitals and a line with end as the first 3 characters.
3.3.8 Orbitals with non standard options Item 32
-
OPTION
- to modify the standard options for some of the orbitals. Must be y or n.
-
- Only if option is y:, for each orbital to be modified:
-
LABEL :
- label of the orbital for which modifications are requested.
-
IDOI :
- define the type of initial orbital (see definition of NDEP in Item 27)
-
ZH :
- only if IDOI=2, screening of the nuclear charge for hydrogenic initial orbital.
-
numfil :
- only if IDOI=3: record number in file ibb to use to read this orbital. if numfil < 0, set to
the same value as NLEC.
-
indsol(1) :
- select method of solving the Dirac equation. (1=normal case; 3=when frozen orbitals
are involved; 4=for correlation orbitals; 5 for using spline package this method may be
tricky to use, be sure to know what you are doing). Projection operators to exclude
negative-energy continuum are included or not depending on the switch from Item 23.
-
indsol(2) :
- if > 0 use deferred correction. If 0 use the solution of previous iteration to calculate
deferred correction. (0)
-
indsol(3) :
- if 0 enforce number of nodes of radial functions. If 2 check the sign of the slope at
origin for method 5.(0)
-
indsol(4) :
- if not 0 use Schmidt orthogonalization before solving the Dirac equation. (0)
-
indsol(5) :
- if not 0, use Rayleigh quotient to obtain an estimate of the one-electron eigenvalue; if
0 use previous value. (0)
-
indsol(6) :
- if 0 use full exchange; if not, reduce exchange by the coefficient given in Item 26,
ACCF(2,N). (0)
-
icho5 :
- (Only if indsol(1)=5) Choose one of the bound solutions of the spline method. If (0)
use the lower one, else use the icho5-th one or the first available below if there are not enough
solutions
-
scew :
- initial value of the mixing coefficient of the orbital between two iterations. (0.3)
a line with end as the first 3 characters.
3.3.9 Off-diagonal Lagrange multipliers Item 33
-
OPTION
- to modify method of computing off-diagonal Lagrange multipliers. Must be y or n.
-
- Only if option is y:
-
TESTEP :
- criteria to switch from difference method to sum method (0.001)
For each Lagrange multiplier:
-
LABOI(1), LABOI(2) :
- labels of the orbitals involved in the Lagrange multiplier.
-
N :
- selection of the method to compute Lagrange multiplier. (-1)
N< -1: difference method.
N= -1: difference or sum method depending upon occupation numbers.
N= 0: do not compute Lagrange multiplier.
N= 1: sum method.
N> 1: Rayleigh quotient.
a line with end as the first 3 characters.
3.3.10 BSplines for RCI Item 34
Only if KEYWORD in 4th set is rci
-
BSPLINE
- Number of BSPline in the basis set for rci calculation.
-
KSPLINE
- number of collocation points for the BSplines
-
- Only if modrci=y
-
- Labels of the lower n orbital for which one starts to use BSpline basis to provide the radial wave
function (one for each symmetry) and a line with end as the first 3 characters.
3.3.11 Configuration weights Item 35
-
- Note If the keyword ALL has been associated to the option NEIGV=0 the data below will be
used for all eigenvalues
-
- Only if absolute value of ICMUL=1, for each configuration for which the weights have to be read:
-
I :
- configuration index.
-
CW :
- initial coefficient of the configuration.
-
- Note that some of the weights may already have been read from file.
3.3.12 Small configuration weights Item 36
-
- Note If the keyword ALL has been associated to the option NEIGV=0 the data below will be
used for all eigenvalues
-
- Only if ICMUL= 3
-
CWTHRES :
- replacement threshold for mixing coefficients: After first diagonalization, all
coefficient lower than CWTHRES are replaced.
-
CWREP :
- replacement value for mixing coefficients. The sign from the diagonalization are kept.
3.3.13 Use SCF wave functions for more extensive outputs
-
- Note If the keyword ALL has been associated to the option NEIGV=0 the data below will be
used for all eigenvalues
Which outputs are wanted Item 37
-
input(1) :
- if not 0, Coulomb or Breit integrals are calculated.
-
input(2) :
- if not 0, one-electron integrals are calculated.
-
input(3) :
- if not 0, expectation values of r**n are calculated.
-
input(4) :
- if not 0, one-electron radial wavefunctions are tabulated.
-
input(5) :
- if not 0, total density is written to file with Fortran number IPUN. Furthermore if > 0
total density is also written to the standard output file.
-
input(6) :
- number of radial wavefunctions to be written on file with Fortran number ipun.
-
input(7) :
- if not 0 coefficients of the series expansions near the origin are tabulated.
-
input(8) :
- if not 0 direct potential is printed for all orbitals.
-
input(9) :
- if not 0, the Coulomb and vacuum polarization potentials are printed.
-
input(10) :
- if not 0, the mean value of a
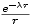 is evaluated for all orbitals.
is evaluated for all orbitals.
Coulomb and/or Breit integrals Item 38
-
- Only if INPUT(1) is not 0:
-
LABELI(I) I=1 to 4:
- label of the orbitals involved in the integral.
-
K:
- power of the multipole
-
NEM:
- if 0 Coulomb integral and Breit integral otherwise. Furthermore if < 0 integration over
variable S is from 0 to R only. The integrals are defined as: integral over R and S of:
F(R) * UK(R,S) * G(S) with:
| F = P1 * P2 + Q1 * Q2 | G = P3 * P4 + Q3 * Q4 | if NEM=0 |
| F = P1 * Q2 | G = P3 * Q4 | if NEM not 0 |
| |
a line with end as the first 3 characters.
One-electron integrals Item 39
-
- Only if INPUT(2) is not 0:
-
LABELI(I) I=1,2:
- label of the orbitals involved in the integral.
-
IALL:
- if not 0 all one-electron integrals are calculated starting from the one defined by the first
label.
a line with end as the first 3 characters.
Expectation values of rn Item 40
-
- Only if INPUT(3) is not 0:
-
LABELI(I) I=1,2:
- label of the orbitals involved in the integral.
-
N:
- power of r.
-
NEM:
- integral is:
(P1 * P2 + Q1 * Q2)rN if NEM=0
(P1 * Q2 + P2 * Q1)rN if NEM not 0
-
IALL:
- if greater than 0 (lower than 0) all integrals (only the diagonal ones) are calculated starting
from the one defined by the first label.
a line with end as the first 3 characters.
Labels of the orbitals to be written Item 41
-
- Only if INPUT(6) is not 0:
-
LABELI(I) I= 1 to INPUT(6):
- labels of the orbitals to be written on file ipun.
Parameters of the Yukawa potential Item 42
-
- Only if INPUT(10) is not 0:
-
APAR:
- relative interaction strength.
-
LAMBDA:
- interaction range in atomic unit.
3.3.14 Specific data for Born cross section: Item 43
To be given only for electron impact Born excitation cross section
-
q1:
- first value for the grid to integrate over momentum transfert. (0.0001)
-
hqm:
- mesh for the grid to integrate over momentum transfert. (0.04)
-
INCIDENT ENERGIES:
- values for the electron incident energy (in eV)
3.3.15 End of input data: Item 44
Two asterisks as the first 2 characters.
3.4 Subroutines reading input data
| Items | read by subroutine |
| 1 to 3 | ini_at1 |
| 4 | ini_at2 |
| 5 to 17 | in1_mcdfgme |
| 18 | nucpot_par |
| 19 and 20 | in2_mcdfgme |
| 21 | cfgread_bld |
| 22 and 24 | in2_mcdfgme |
| 25 | in3_mcdfgme |
| 26 to 34 | in4_mcdfgme |
| 35 and 36 | inmcdf |
| 37 to 42 | uwfrdf |
| 43 | borgme |
| 44 | ini_at2 |
| |
Chapter 4
SELECTED EXAMPLES OF INPUT DATA
4.1 Test case for energy calculation with BSpline solution for correlation orbital
Test case for energy calculation only, use spline method for correlation orbital, with projection operator
and both full Breit interaction and vacuum-polarization self-consistant
mdfgme.dat input file
testhe-like.f05 input file
*801 he-like 1s2 z=54
scfmdf max els2am max hdimdf max :
mod_lightspeed=n
nz=54
mdf do_ener=y keep_ener=n binary_ener=y do_scf=y
Breit=full mag_scf=y ret_scf=y
vacpol_scf=y
energy
ret_Lorentz=y
opt_qedel=y :
mod_mesh=n
exotic=n
mod_nuc=n
nbel=2
def_config=given
c 1 1s2 :
end
jjt=0 mjt=0
negative_continuum=y
neigv=1 icmul=0 iprfgr=1
norbsc=00 ndep=0 nlec=0 nec=1 :
nstep=0
lregul=n modtest=n
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
*802 he-like 1s2+2s2 z=54
scfmdf max els2am max hdimdf max :
mod_lightspeed=n
nz=54
mdf do_ener=y keep_ener=n binary_ener=y do_scf=y
Breit=full mag_scf=y ret_scf=y
vacpol_scf=y
energy
ret_Lorentz=y
opt_qedel=y :
mod_mesh=n
exotic=n
mod_nuc=n
nbel=2
def_config=given
c 1 1s2 :
c 2 2s2 :
end
jjt=0 mjt=0
negative_continuum=y
# check threshold for mixing coefficients
neigv=1 icmul=3 iprfgr=1
# read 1s wavefunction from previous case
norbsc=00 ndep=3 nlec=1 nec=0 0 0 1 :
nstep=0
lregul=n modtest=n
modsolv_orb=y
2s 1 5 0 1 :
end
mod_odlm=n
# threshold and replacement values for mixing coefficients
cwthresh=1.E-3 cwrep=1.5E-3
# data for uwfrdf
:
**
|
4.2 Test case for energy calculation followed by transition rate evaluation
mdfgme.dat input file
testprob.f05 input file
*tm1 he-like 1s2s->1s2 M1 z=54
:
mod_lightspeed=n
nz=54
mdf do_ener=y keep_ener=n binary_ener=y do_scf=y
Breit=full mag_scf=y ret_scf=y
vacpol_scf=y
magnetic ipol=1
use_mcdfener=n eexp=30127.3 eV sub_offset=n
opt_relax=y
ret_Lorentz=y
opt_qedel=y :
mod_mesh=n
exotic=n
mod_nuc=n
nbeli=2 nbelf=2
def_config=given
c 1 (1s1])1 (2s1])1 :
end
c 1 (1s2])2 :
end
jjti=2 mjti=2
jjtf=0 mjtf=0
negative_continuum=n
# initial state parameters
neigv=1 icmul=0 iprfgr=0
norbsc=00 ndep=0 nlec=0 nec=1 :
nstep=0
lregul=n modtest=n
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
#final state parameters
neigv=1 icmul=0 iprfgr=0
norbsc=00 ndep=0 nlec=0 nec=2 :
nstep=0
lregul=n modtest=n
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
**
|
4.3 Test case for energy calculation followed by hyperfine matrix element calculation. Case with
diagonal and non diagonal matrix elements appears in the same file.
mdfgme.dat input file
testhfs.f05 input file
*805 diagonal hydrogenlike Bi 1s HFS
:
mod_lightspeed=n
nz=83
mdf do_ener=y keep_ener=n binary_ener=y do_scf=y
Breit=full mag_scf=y ret_scf=y
vacpol_scf=y
hyperfine ipol=1 inuc=9 gnuc=4.1106 diagonal=y
ret_Lorentz=y
opt_qedel=y :
mod_mesh=y
hx=0.025 :
exotic=n
mod_nuc=y
A=209 rms=5.518 ferc=2.0566022 nuc=101
nbeli=1
def_config=given
c 1 (1s2])1 :
end
jjtf=1 mjtf=1
negative_continuum=n
# initial state parameters
neigv=1 icmul=0 iprfgr=0
norbsc=00 ndep=0 nlec=0 nec=1 :
nstep=0
lregul=n modtest=n
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
*807 Non-diagonal gold he-like 1s2p 3P1-3P0
maelam max operam max hfsgme max :
mod_lightspeed=n
nz=79
mdf do_ener=y keep_ener=n binary_ener=y do_scf=y
Breit=full mag_scf=y ret_scf=y
vacpol_scf=y
hyperfine ipol=1 inuc=3 gnuc=0.14486 diagonal=n
opt_relax=n
ret_Lorentz=y
opt_qedel=y :
mod_mesh=n
exotic=n
mod_nuc=n
nbeli=2 nbelf=2
def_config=given
c 1 (1s1])1 (2p1])1 :
end
c 1 (1s1])1 (2p1])1 :
end
jjti=2 mjti=2
jjtf=0 mjtf=0
negative_continuum=n
# initial state parameters
neigv=1 icmul=0 iprfgr=0
norbsc=00 ndep=0 nlec=0 nec=1 :
nstep=0
lregul=n modtest=n
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
# final state parameters
neigv=1 icmul=0 iprfgr=0
norbsc=00 ndep=0 nlec=0 nec=2 :
nstep=0
lregul=n modtest=n
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
**
|
4.4 Test case for energy calculation on a pionic and an antiprotonic atom
mdfgme.dat input file
testpbar.f05 input file
*809 Exotic: pion 1s1/2 2p@
eneram_det max :
mod_lightspeed=n
nz=6
mdf do_ener=y keep_ener=n binary_ener=y do_scf=y
Breit=full mag_scf=n diag_afterscf=n
vacpol_scf=y
energy
ret_Lorentz=n
opt_qedel=n :
mod_mesh=y
hx=0.02 r(1)=0.01 amesh=0.1 :
exotic=y pion
mod_nuc=n
nbel=2
def_config=given
c 1 (1s)1 (2p@])1 :
end
jjt=1 mjt=1
negative_cont=n
part_finsize=y
neigv=1 icmul=0 iprfgr=1
norbsc=00 ndep=0 nlec=0 nec=0 0 0 1 :
nstep=0
lregul=n modtest=n
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
*818 Exotic: pbar 1s1/2 (6h@])
:
mod_lightspeed=n
nz=2
mdf do_ener=y keep_ener=n binary_ener=y do_scf=y
Breit=full mag_scf=n diag_afterscf=n
vacpol_scf=y
gm2p
inuc=41 gnuc=1.0 diag=y
ret_Lorentz=n
opt_qedel=n :
mod_mesh=y
hx=0.021 r(1)=0.01 amesh=0.2 :
exotic=y pbar
mod_nuc=n
nbel=2
def_config=given
c 1 (1s)1 (6h@])1 :
end
jjt=12 mjt=12
negative_cont=n
part_finsize=y
neigv=1 icmul=0 iprfgr=1
norbsc=00 ndep=0 nlec=0 nec=1 0 0 1 :
nstep=0
lregul=n modtest=y
teste=1.e-7 rap=1000. :
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
*819 Exotic: pbar 1s1/2 (39+35[@])
:
mod_lightspeed=n
nz=2
mdf do_ener=y keep_ener=n binary_ener=y do_scf=y
Breit=full mag_scf=y ret_scf=n diag_afterscf=n
vacpol_scf=y
energy
ret_Lorentz=n
opt_qedel=n :
mod_mesh=y
hx=0.021 r(1)=0.01 amesh=0.2 :
exotic=y pbar
mod_nuc=n
nbel=2
def_config=given
c 1 (1s)1 (39+35[@])1 :
end
jjt=72 mjt=72
negative_cont=n
part_finsize=n
neigv=1 icmul=0 iprfgr=1
norbsc=00 ndep=0 nlec=0 nec=0 0 0 1 :
nstep=0
lregul=n modtest=y
teste=1.e-7 rap=1000. :
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
**
|
4.5 Test case for RCI calculation
mdfgme.dat input file
testrci.f05 input file
*826 he-like 1s2p 3P1 z=83 preparation for RCI example
:
mod_lightspeed=n
nz=83
mdf do_ener=y keep_ener=n binary_ener=y do_scf=y
Breit=full mag_scf=n diag_afterscf=n
vacpol_scf=n
energy
ret_Lorentz=y
opt_qedel=n :
mod_mesh=n
exotic=n
mod_nuc=n
nbel=2
def_config=given
1 (1s)1 (2p)1 :
end
jjt=2 mjt=2
negative_continuum=y
neigv=1 icmul=0 iprfgr=0
norbsc=00 ndep=0 nlec=0 nec=1 :
nstep=0
lregul=n modtest=n
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
*827 he-like 1s2p 3P1 z=83 rci nsn'p z=83, coulomb, short example
:
mod_lightspeed=n
nz=83
rci do_ener=y keep_ener=n binary_ener=y do_scf=y modrci=y
Breit=full mag_scf=n diag_afterscf=n
vacpol_scf=n
energy
ret_Lorentz=y
opt_qedel=n :
mod_mesh=n
exotic=n
mod_nuc=n
nbel=2
def_config=given
1 (1s)1 (2p)1 :
2 (2s)1 (2p)1 :
3 (2p)1 (3s)1 :
4 (1s)1 (3p)1 :
5 (2p)1 (4s)1 :
6 (1s)1 (4p)1 :
7 (2p)1 (5s)1 :
8 (1s)1 (5p)1 :
end
jjt=2 mjt=2
negative_continuum=y
neigv=1 icmul=0 iprfgr=1
norbsc=00 ndep=3 nlec=1 nec=2 :
nstep=0
lregul=y modtest=n
modsolv_orb=n
mod_odlm=n
# since modrci=y, list of orbitals to be generated with BSplines
BSpline=19 kspline=5
# list the first orbital (lower nq) that will be generated by BSplines
2s 3p* 3p :
end
# data for uwfrdf
:
**
|
4.6 Test case for Born cross section calculation
mdfgme.dat input file
testborn.f05 input file
*b01 Be 1s2 -> 1s2p 1P1 Born cross section
:
mod_lightspeed=n
nz=4
mdf do_ener=y keep_ener=n binary_ener=y do_scf=y
Breit=full mag_scf=n diag_afterscf=y keep_scfcoeff=y
vacpol_scf=n
born
use_mcdfener=n eexp=5.277433 eV
opt_relax=n
ret_Lorentz=n
opt_qedel=n :
mod_mesh=n
exotic=n
mod_nuc=n
nbeli=4 nbelf=4
select_cfg=given
c 1 1s2 2s2 :
end
c 1 1s2 2s1 2p1 :
end
jjti=0 mjti=0
jjtf=2 mjtf=2
negative_continuum=n
# initial state parameters
neigv=1 icmul=0 iprfgr=0
norbsc=00 ndep=0 nlec=0 nec=1 :
nstep=0
lregul=n modtest=n
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
#final state parameters
neigv=2 icmul=0 iprfgr=0
norbsc=00 ndep=0 nlec=0 nec=2 :
nstep=6
1 1 50 4. 0.01 0.90 1.0 1.0
1 1 50 4. 0.001 0.90 1.0 1.0
1 1 50 4. 0.0001 0.95 1.0 1.0
1 1 50 4. 0.00001 0.95 1.0 1.0
1 1 50 4. 0.00001 1.00 1.0 1.0
1 1 50 4. 0.000001 1.00 1.0 1.0
lregul=n modtest=n
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
# this the beginning of specific input data for Born cross section
# first optional options to buils the Q grid
:
# followed by values of incident energy
TEV=6. 7. 8. 9. 10. 20. 50. 100.
500. 1000. :
**
|
4.7 Test case for overlaps for shake-off
mdfgme.dat input file
shakeoff.f05 input file
*811 shake-off Xe 50+ 1s2 2s2+excit -> 1s 2s (wavefunction must be 1s 2s2 in file)
:
mod_lightspeed=n
nz=54
mdf do_ener=y keep_ener=n binary_ener=y do_scf=y
Breit=full mag_scf=y ret_scf=y
vacpol_scf=y
shakeoff
relax=y
ret_Lorentz=y
opt_qedel=y :
# ":" above is for ilams taken to be the default value
mod_mesh=n
exotic=n
mod_nuc=n
nbeli=4 nbelf=3
select_cfg=given
1s2 2s2 :
end
1s1 2s2 :
end
jjt=0 :
jjt=1 :
negative_continuum=n
# initial state parameters
neigv=0 all icmul=0 iprfgr=0
norbsc=0
ndep=0 nlec=0 nec=1 :
nstep=0
lregul=n modtest=n
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
# initial state parameters
neigv=0 all icmul=0 iprfgr=0
norbsc=0
ndep=0 nlec=0 nec=2 :
nstep=0
lregul=n modtest=n
modsolv_orb=n
mod_odlm=n
# data for uwfrdf
:
**
|
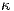
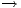 n'
n'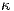 ). IF y Brillouin excitation will be included, but convergence then may be very
difficult.
). IF y Brillouin excitation will be included, but convergence then may be very
difficult.
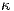
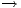 n'
n'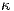 ). IF y Brillouin excitation will be included, but convergence then may be very
difficult.
). IF y Brillouin excitation will be included, but convergence then may be very
difficult.
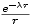 is evaluated for all orbitals.
is evaluated for all orbitals.